DISTRIBUCIÓN DE BERNOULLI
Distribución de Bernoulli La distribución de Bernoulli de parámetro p es el modelo más simple de probabilidad.Se aplica a situaciones en las que un cierto atributo aparece con probabilidad p (éxito) y laausencia de este mismo atributo con probabilidad q=1-p (fracaso), como en el lanzamientode una moneda. Que puede dar como resultado cara o cruz.
Recíprocamente, todo experimento aleatorio que sólo admite dos resultadosposibles, (uno llamado por costumbre éxito y el otro fracaso) se llama ensayo deBernoulli y lleva obviamente a la distribución de Bernoulli.
Por ejemplo:
Un tratamiento médico puede ser efectivo o inefectivo.
La meta de producción o ventas del mes se pueden o no lograr.
En pruebas de selección múltiple, aunque hay cuatro o cinco alternativas, se pueden clasificar como correcta o incorrecta.
Su formula es: p[X = x]= p[1 - p]1-^, x = 0.1
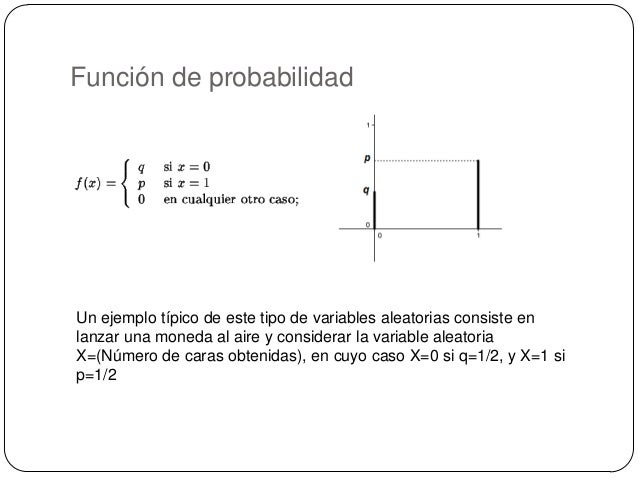
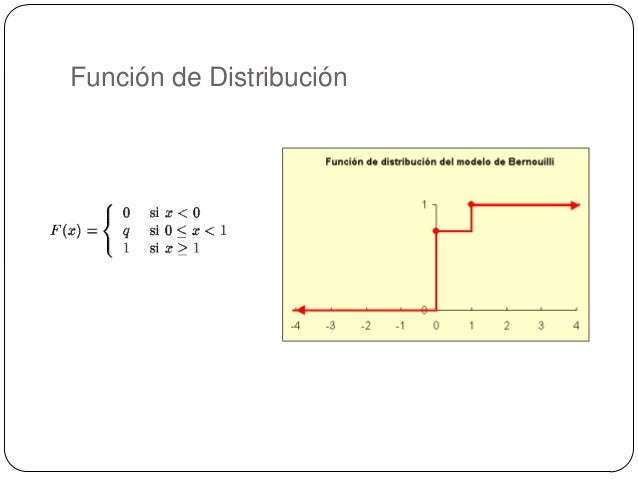
Función de Distribución
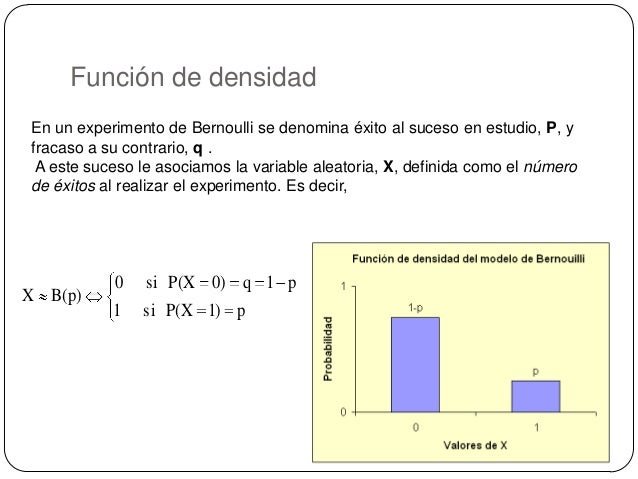
Función de densidad
Experimento Lanzar un dado y que salga 5
X = # de veces que sale un 5.
Al lanzar un dado tenemos 6 posibilidades resultados el espacio muestral es de
S=(1,2,3,4,5,6)
Se considera éxito sacar un 5 entonces la probabilidad es de P=1/6
Se considera fracaso a no sacar un 5 entonces q= 1-P = 1-(1/6) = 5/6
La probabilidad de que salga un 5 viene definida en que x =1 (éxito)
P(x=1) = (1/6)1 * (5/6)1-1 = 1/6 = 0.16
Y x=0 (fracaso) p[X = x]= p[1 - p]1-^, x = 0.1
P(x=0) = (1/6)0 * (5/6)1-0 = 5/6 = 0.83
Comentarios
Publicar un comentario